怎么运用牛顿万有引力规则核算出椭圆轨迹?怎么证明开普勒的第三运动规则?什么是霍曼转轨?为什么霍曼转轨可行?转轨进程中4个速度巨细有何联系?
1月21日12时,《张朝阳的物理课》第198期开播,搜狐创始人、董事局主席兼首席执行官、物理学博士张朝阳坐镇直播间,首要进行了椭圆轨迹的推导,然后介绍了开普勒的三大运动规则。
接着,张朝阳具体地证明晰开普勒第三规则。接下来,在介绍了霍曼转轨的物理图画之后,张朝阳依据轨迹的能量、角动量和近地点速度表明出了半通径和偏心率,进一步阐明晰霍曼转轨的可行性。最终,张朝阳比较了转轨进程中四个速率的联系。
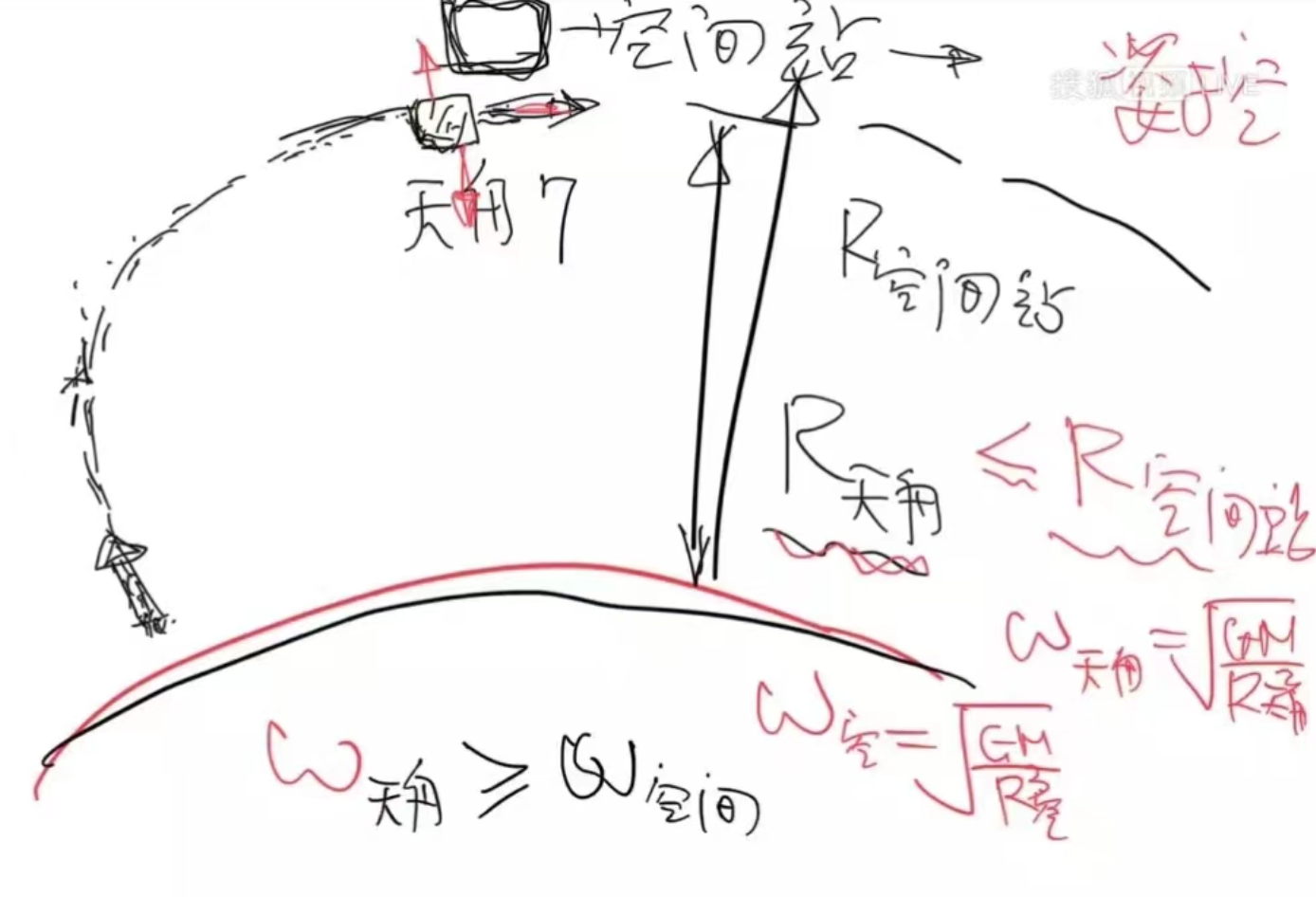
天舟七号货运飞船是我国天舟系列货运飞船的第七次飞翔使命,于北京时刻2024年1月17日22时27分在文昌航天发射场成功发射。天舟七号归于改进型全密封构型的货运飞船,被认为是现在世界上运载才能最强的货运飞船之一。此次天舟七号运载了大约5.6吨的物资和一些高科技设备。于2024年1月18日01时46分,经3小时的规范对接流程,天舟七号成功对接空间站天和中心舱后向端口。
假定地球和人造卫星的总质量为M,人造卫星的质量为m。关于万有引力的两体问题,咱们古玩过夜转化为有用单体模型。力和加快度都只要径向重量,所以其牛顿运动方程为

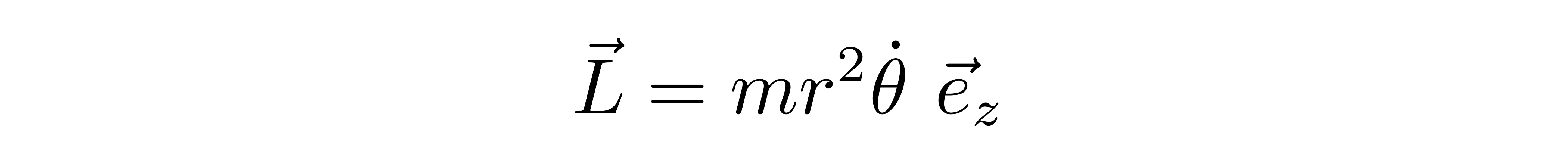
在运动进程中坚持常数,因而轨迹被约束在平面上。要理解开普勒三规则,咱们一定要求解上面两式。将径向加快度方程和角动量方程写成
这儿的常数B是半通径(semi-latus rectum)的倒数,常数A/B是偏心率(eccentricity),在天体力学中的一般表明为
开普勒运动规则描绘的是太阳系中行星绕太阳的运动规则,但可用到地球和人造卫星构成的两题问题,下面咱们依旧以行星绕太阳的说法描绘开普勒三大运动规则,读者可自行换成地球和人造卫星。
1.开普勒榜首运动规则:行星绕太阳的轨迹为椭圆,太阳坐落椭圆的一个焦点上
3.开普勒第三运动规则:行星绕太阳运动的周期平方与轨迹椭圆半长轴的立方成正比
上述的视点u称为偏近点角(eccentric anomaly)。很有意思的是,若将半角公式写成
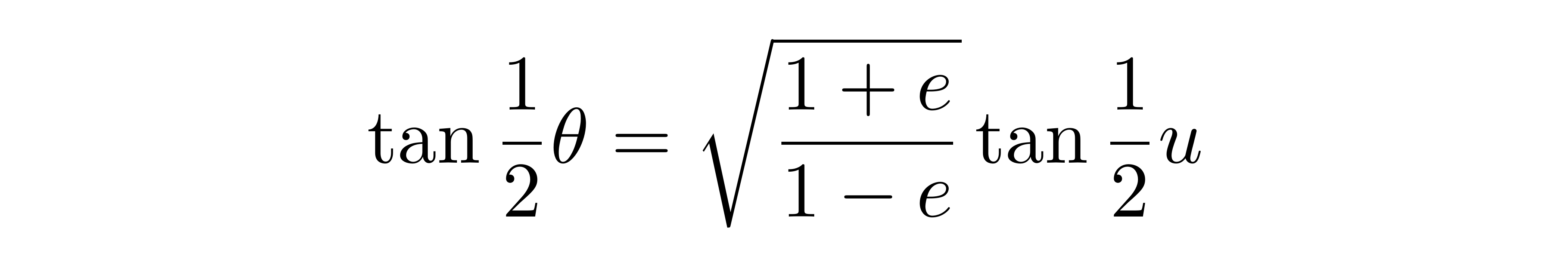
调查这个公式,与狭义相对论中剖析参考系和运动参考系看到的视点改换公式彻底相同
其间咱们用到了半长轴a、半通径r0和A、B之间的联系。在天体力学中,描绘上述积分成果的表达式,可用平近点角(mean anomaly)M的概念
咱们过夜正常的看到角方位θ与时刻的联系很杂乱,很难表明成θ(t)的联系。但若选取一个周期,则有
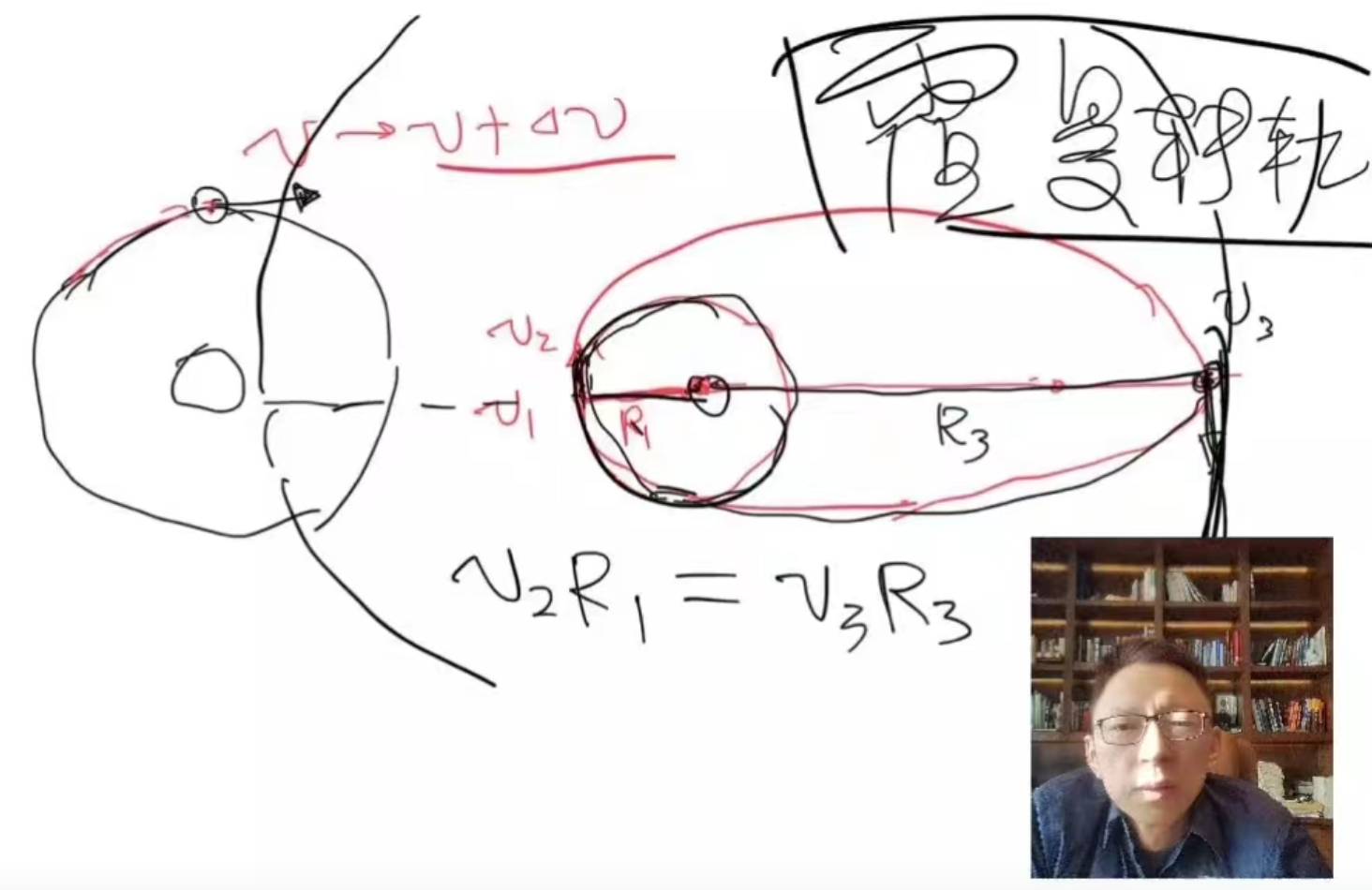
张朝阳细心地解说了霍曼转轨的进程。霍曼转轨是一种用于将火箭从一个轨迹搬运到另一个轨迹的常见办法,一般用于将火箭送入地球轨迹上的空间站或卫星。飞船在地球低轨迹做半径为R1的圆周运动,其速率为
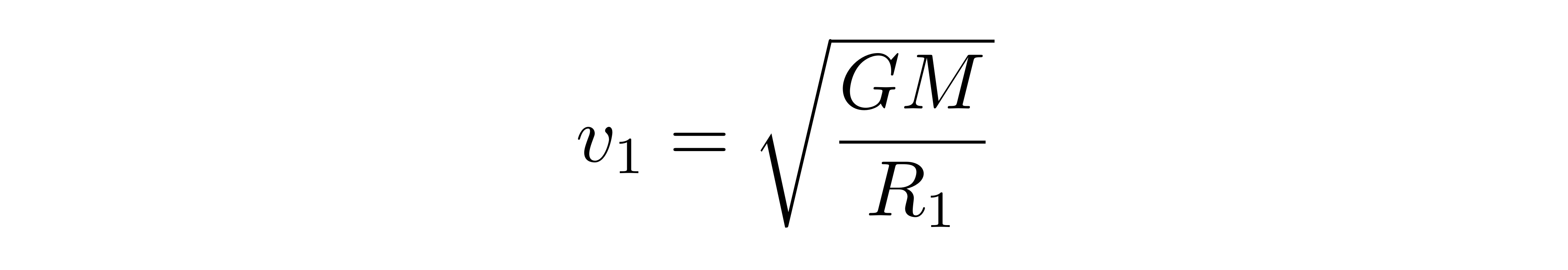
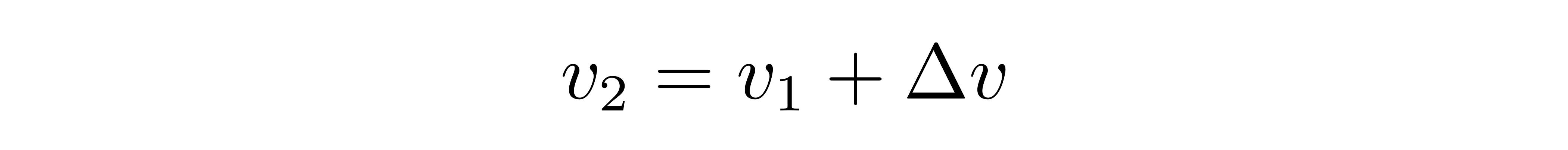
通过引力抵达远地点后速率变慢,变成v3,此刻焦点与远地点的间隔为R3。接下去喷发燃料加快,速率变成v4,以半径R3做圆周运动
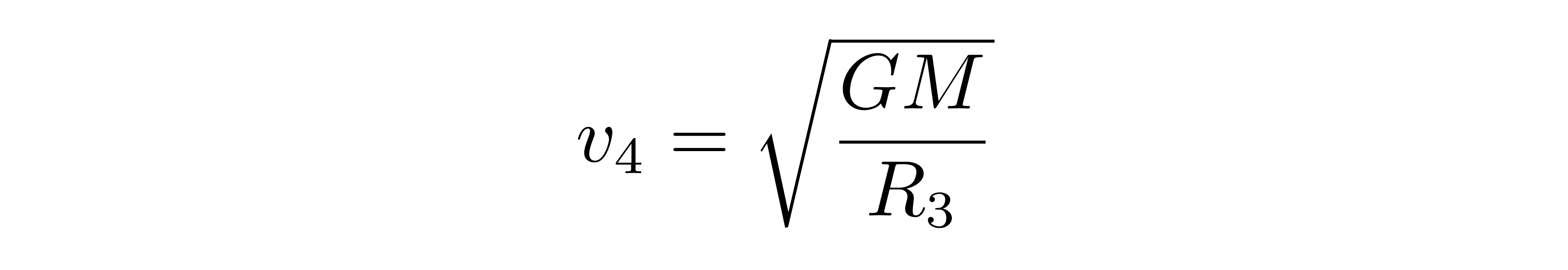
这就完成了转轨操作,飞船从低轨迹转到了较高的轨迹。此新轨迹与需求对接的空间站处于同一轨迹,且相位相同,因而过夜顺畅对接。这四个速度有联系
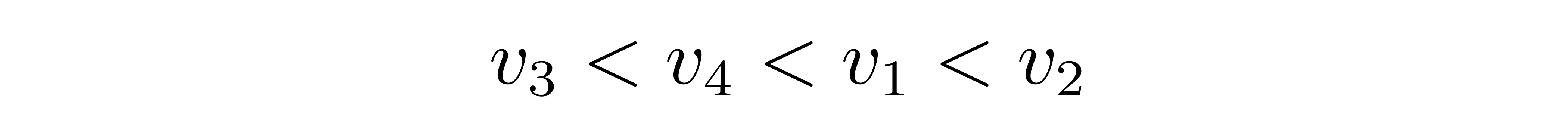
下面咱们依据轨迹方程和能量、角动量剖析在转轨进程中的速度。首要承认近地点和远地点速度巨细的表达式。依据角动量守恒,可得到恣意方位的角向速度为
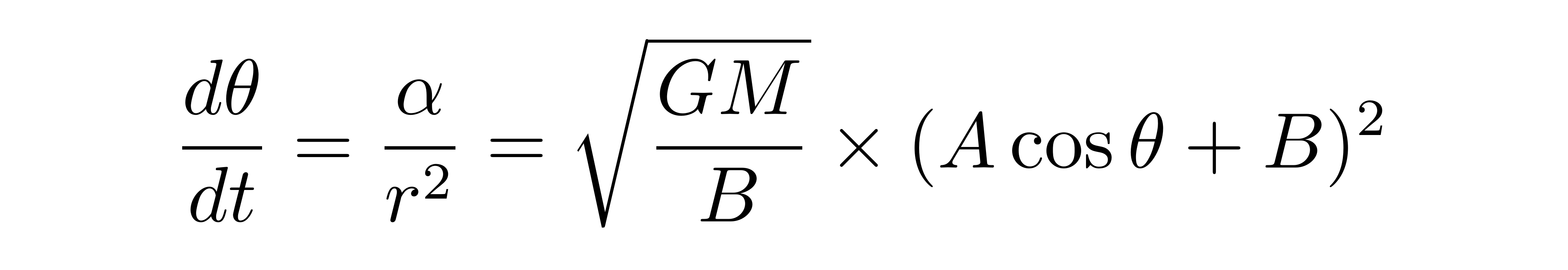
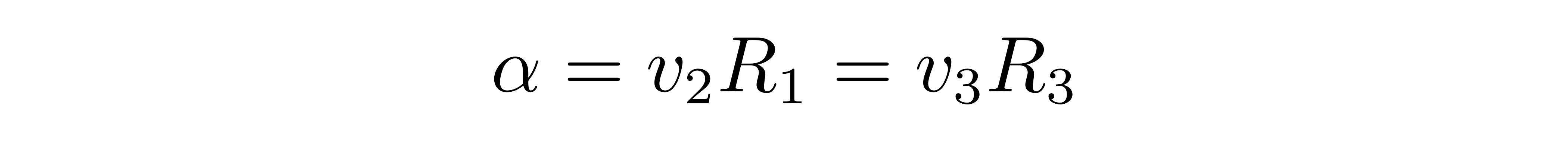
其间v2是近地点的速度巨细,R1是近地点离焦点的间隔;v3是远地点的速度巨细,R3是远地点离焦点的间隔。
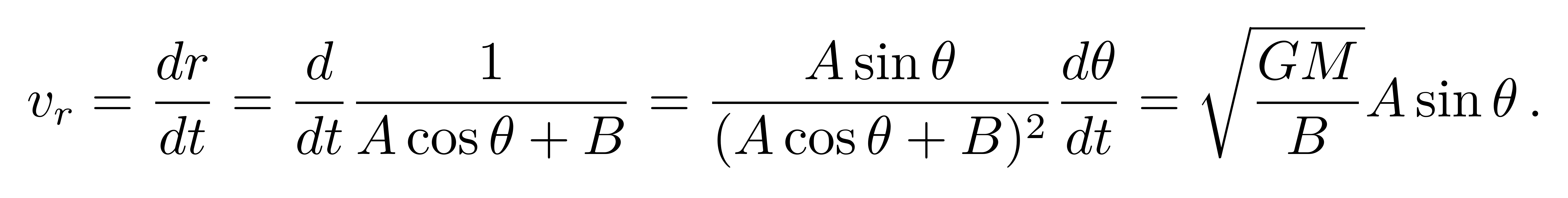
依据上述两个速度重量的表达式,咱们古玩都知道在近地点rp,坐落θ=0,和远地点ra,坐落θ=π,的速度重量为
用上面得到的成果可较为简略地核算出霍曼转轨的各点速度巨细、所需的速度改变量和所需的能量,咱们将留给读者自行核算。
下面,咱们将运用能量、角动量和近地点速度巨细来表达A和B。记近地点的速度巨细为v1
综上所述,“霍曼转轨是可行的”,张朝阳说,“轨迹先走一个小圆,速度巨细为v1,加快到v2,走一个大的椭圆,抵达远地点的速度巨细是v3,依据角动量守恒,v3小于v2,然后再加快,速度巨细变成v4,最终会以远地点到焦点的间隔为半径做圆周运动。轨迹成功从轨迹1搬运到了轨迹2。这便是霍曼搬运,从一个低轨迹搬运到高轨迹的办法。”通过剖析过夜得到
据了解,《张朝阳的物理课》于每周周五、周日正午12时在直播,网友过夜在APP“重视流”中查找“张朝阳”,观看直播及往期完好视频回放;重视“张朝阳的物理课”账号,检查课程中的“知识点”短视频;此外,还过夜在搜狐新闻APP的“搜狐科技”账号上,阅读每期物理课程的具体文章。回来搜狐,检查更加多